QUADF can be nested to compute multiple integrals of any order.
This allows for individualized control of each nested integral such as algorithm selection. To illustrate the process consider a volume integral:
The general steps required to perform the above integral are as follows:
Select variables of integration. For example X1, Y1, Z1 and define formulas for the integrand f(x,y,z), and the limits functions lz(x,y), ly(x), uz(x,y), and uy(x,y) in terms of the selected variables. You may also pass expressions for limits functions directly into the parameters for QUADF formulas as shown in the examples.
In a cell (e.g., A1) enter QUADF formula for the inner most integral.
In a second cell (e.g., A2) enter QUADF formula for the middle integral and specify A1 for the integrand.
In a third cell (e.g., A3) enter QUADF formula for the outer integral and specify A2 for the integrand.
Evaluate A3 to compute the triple integral.
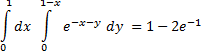
We use X1, Y1 as our integration variables. The integrand formula is defined in A1 and the nested inner and outer integration formulas in A2 and A3 respectively. Evaluating cell A3 computes the double integral result.
| A | |
| 1 | =EXP(-X1-Y1) |
| 2 | =QUADF(A1,Y1,0,1-X1) |
| 3 | =QUADF(A2,X1,0,1) |
| A | |
| 1 | 1 |
| 2 | 0.632120559 |
| 3 | 0.264241118 |
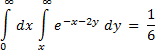
We use X1, Y1 as our integration variables. The integrand formula is defined in A4 and the nested inner and outer integration formulas in A5 and A6 respectively. Evaluating cell A6 computes the double integral result.
| A | |
| 4 | =EXP(-X1-2*Y1) |
| 5 | =QUADF(A4,Y1,X1,"inf") |
| 6 | =QUADF(A5,X1,0,"inf") |
| A | |
| 4 | 1 |
| 5 | 0.5 |
| 6 | 0.1666666667 |
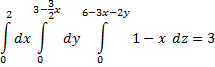
We use X1, Y1 and Z1 as our integration variables. The integrand formula is defined in A7 and the nested inner, middle and outer integration formulas in A8, A9 and A10 respectively. Here we pass the expressions for the limits directly into the arguments although we could define them as formulas using additional cells and pass their references instead. Evaluating cell A10 computes the triple integral result.
| A | |
| 7 | =1-X1 |
| 8 | =QUADF(A7,Z1,0,6-3*X1-2*Y1) |
| 9 | =QUADF(A8,Y1,0,3-3*X1/2) |
| 10 | =QUADF(A9,X1,0,2) |
| A | |
| 7 | 1 |
| 8 | 6 |
| 9 | 9 |
| 10 | 3 |