ExceLabTM 7.0
Calculus Functions Powerhouse Add-in

Patented Library of Calculus Spreadsheet solvers for Microsoft Excel and Google Sheets

For Windows PCs, Apple Macs and Online


Windows OS

ExceLab 7.0

Windows PC. All Office versions

Mac & Office 365

ExceLab 365

Apple Mac; Office 365; Excel Online

Install from Microsoft AppSource
In your Excel click Install → Get Add-ins
Microsoft 365 account is required
Google Sheets

ExceLab Sheets

Google Sheets Calculus Add-on


Solve complex calculus problems with simple formulas

Numerical Integration Demo.

  • ✔Expand Excel/Sheets native math function with a super set of powerful solvers.

  • ✔Use the solvers in standard formulas exactly like native math functions.

  • ✔Runs on all localized Windows versions, Apple Macs and online

  • ✔No coding. No learning curves. Just basic Excel spreadsheet skills.

  • ✔Lightweight add in with superfast installation and you are up and running.

  • ✔State of the art proven algorithms that work with superior performance.

  • ✔Share your results workbook easily with your co-workers.

  • ✔Evaluate free to your satisfaction.

  • ✔Get prompt support and answers to questions from our experienced team.

What our users say

See full reviews

"Excelab 7.0 is perfect product, daily used very efficiently while saving unbelievable time in calculations and result analyzing."
"ExcelWorks calculus add-in has been incredibly helpful.... The ExcelWorks support have also been incredibly helpful, responding to any queries I had in a quick and effective manor. I would most definitely recommend this add-in to anyone considering."
".. the ability to share models and results in a highly familiar platform..with near-zero learning-curve in using the program, have compelled me to break from the past and put in the effort to move our models to ExceLab."
"It is easy to learn and support provided by the admin staff is very nice. If anyone working on multi PDEs equation problems, just try this one you will love this solver"
"I found excel-works derivative functions quite useful. I was particularly pleased with the prompt response for assistance when I required some technical issues to be resolved....."
What can you solve with ExceLab

ExceLab is a unique add-in which extends Excel native math functions with a super set of powerful calculus functions. You use these functions in standard or array formulas just like native functions to solve elementary and advanced calculus problems including:

The functions offer you state of the art algorithms to effortlessly and accurately solve calculus problems with just basic spreadsheet skills and no programming. Navigate the Tabs above for quick examples.

Compute numerical integrals

  • Use QUADF to integrate formulas and user defined VBA functions

  • Use QUADXY to integrate (x,y) data points

  • Nest QUADF to compute multiple integrals of any order

  • Highly accurate adaptive algorithms

  • Finite and infinite limits

  • Singular integrands

Quick Example

∫ 0 1 ln x x ⋅ d x =   ?

Solution

A
1=LN(X1)/SQRT(X1)
2=QUADF(A1,X1,0,1)
⇒
A
1#NUM!
2-4

Compute numerical derivatives

  • Use DERIVF to compute derivatives of formulas and VBA functions

  • Use DERIVXY to compute derivatives from (x,y) data points

  • Nest DERIVF to compute partial derivatives of any order

  • First and higher-order derivatives

  • Highly-accurate adaptive algorithm

Quick Example

f(x) = x⁢ sin(x2) +1 f´(π) =   ?

Solution

A
1=X1*SIN(X1^2)+1
2=DERIVF(A1,X1,PI())
⇒
A
11
2-18.248596

Interpolate 2D and 3D data points

  • Use INTERPXY to interpolate scattered 2D (x,y) points

  • Use INTERPXYZ to interpolate scattered 3D (x,y,z) points

  • Map your scattered (x,y) and (x,y,z) onto uniform grids and plot the curve or surface in Excel

  • Best known Natural Neighbour Algorithm

Quick Example: gridding and plotting 3D Scattered points

Scattered (x,y,z) data points
ABC
1xyz
20.1241620.0111090.124162
30.4687300.2297400.747031
.. ↓
510.2222740.0491640.635259
⇒
Evaluate INTERPXYZ array formula in yellow range
EFG..P
100.1→1
20=INTERPXYZ(A2:B51, z, grid_x, grid_y)
30.1
..↓
121
⇒
Highlight and insert Excel Surface plot

Find exact or best solution

  • Use NLSOLVE to solve a system of nonlinear equations

  • Find least error solution to coupled equations and inequalities constraints

  • Find Roots of non-linear equations

  • Proven Levenberg-Marquardt Algorithm

Quick Example

104x1x2-1=0 e-x1+e-x2-1.0001=0 x1,x2 = ?

Solution

Define equations
AX
1=10^4*X1*X2-11
2=EXP(-X1)+EXP(-X2)-1.00011
Solve with NLSOLVE function
AB
4=NLSOLVE(A1:A2,X1:X2)
5
⇒
Result
AB
4X19.10614674
5X21.09816E-05

Solve ordinary differential equations

  • Use IVSOLVE to solve an initial value problem ODE system

  • Use BVSOLVE to solve a boundary value problem ODE system

  • Highly-staple highly-accurate fully-implicit adaptive algorithms

  • Formatted output ready for plotting in Excel

Quick initial value ode example

dxdt=v,    x0=1,  v0=0 dvdt=-2ζωv-ω2x t ∈ [0, 12]

Solution

Define ODE variables and equations
ABCD
2tw1
3x1zeta0.25
4v0
6dx/dt=v
7dv/dt=-2*zeta*w*v-w^2*x
Solve with IVSOLVE function
IJK
1=IVSOLVE(B6:B7,(t,x,v),{0,12})
..
32
⇒
Plot results

Solve partial differential equations

  • Use PDSOLVE or to solve partial differential equations

  • Use PDASOLVE to solve partial differential algebraic equations

  • Robust Method of Lines with adaptive time step

  • Multiple regions with discontinuous properties

  • General boundary conditions

  • Flexible output formats for plotting transient and snapshot views

Quick Example: heat equation

∂u∂t=k∂2u∂x2,  
u0,t= 100, 
ux(1,t)=0, 
ux,0= 100x=00else
t ∈ [0,1], x ∈ [0,1]

Solution

Define PDE variables and equations
ABCD
1tk1
2x
3u=IF(x=0,100,0)
4ux
5uxxLeft BcRight Bc
6du/dt=k*uxx=u-100=ux
Solve with PDSOLVE function
ABCD
8=PDSOLVE(B6,B1:B5,C6,D6,{0,1},{0,1})
..
30
Plot results

Solve dynamical optimization and parameter estimation problems

Numerous Applications

  • Optimize your model parameters for best fit with experimental data

  • Estimate differential equations parameters

  • Maximize or minimize an objective formula subject to dynamic constraints with Excel Solver

See related journal publication Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm.Math. Comput. Appl. 2018, 23, 39.

Quick Example: compute unknown integral limits

f x a b = ∫ a b 1 - x2 + b ⋅ d x

Find a,b such that

f x a b = 8.333333

Solution

Define variables, integral and constraint equations
AB
1a0
2b1
3integrand=1-x1^2+b
4integral=QUADF(B3,X1,a,b)
5constraint=B4-8.333333
Solve constraint equation for a, b with NLSOLVE function
AB
7=NLSOLVE(B5,(a,b))
8
⇒
Results
AB
7a-2
8b3

Solve optimal control problems

A typical optimal control problem has the form:

FInd u(t) and x(t) to maximize (or minimize) a cost index J

J=HxT,T+∫0TGxt,ut,tdt

Subject to

dxdt=fxt,ut,t x0=x0 xT=xT u(t)≤umax

  • Obtain rapid solutions with minimal effort and simple formulas. No programming.

  • Novel structured direct solution procedure combining Excel Solver with the calculus functions.

  • Method applicable to general (non standard) forms of optimal control problems .

  • Remarkable convergence and performance illustrated by several examples.

  • Consistent and sometime better results than complex methods.

See related journal publications

Rapid Solution of Optimal Control Problems by a Functional Spreadsheet Paradigm: A Practical Method for the Non-Programmer. Math. Comput. Appl. 2018, 23, 54.

Novel Spreadsheet Direct Method for Optimal Control Problems. Math. Comput. Appl., 23, 6, 2018.

Video Tutorials

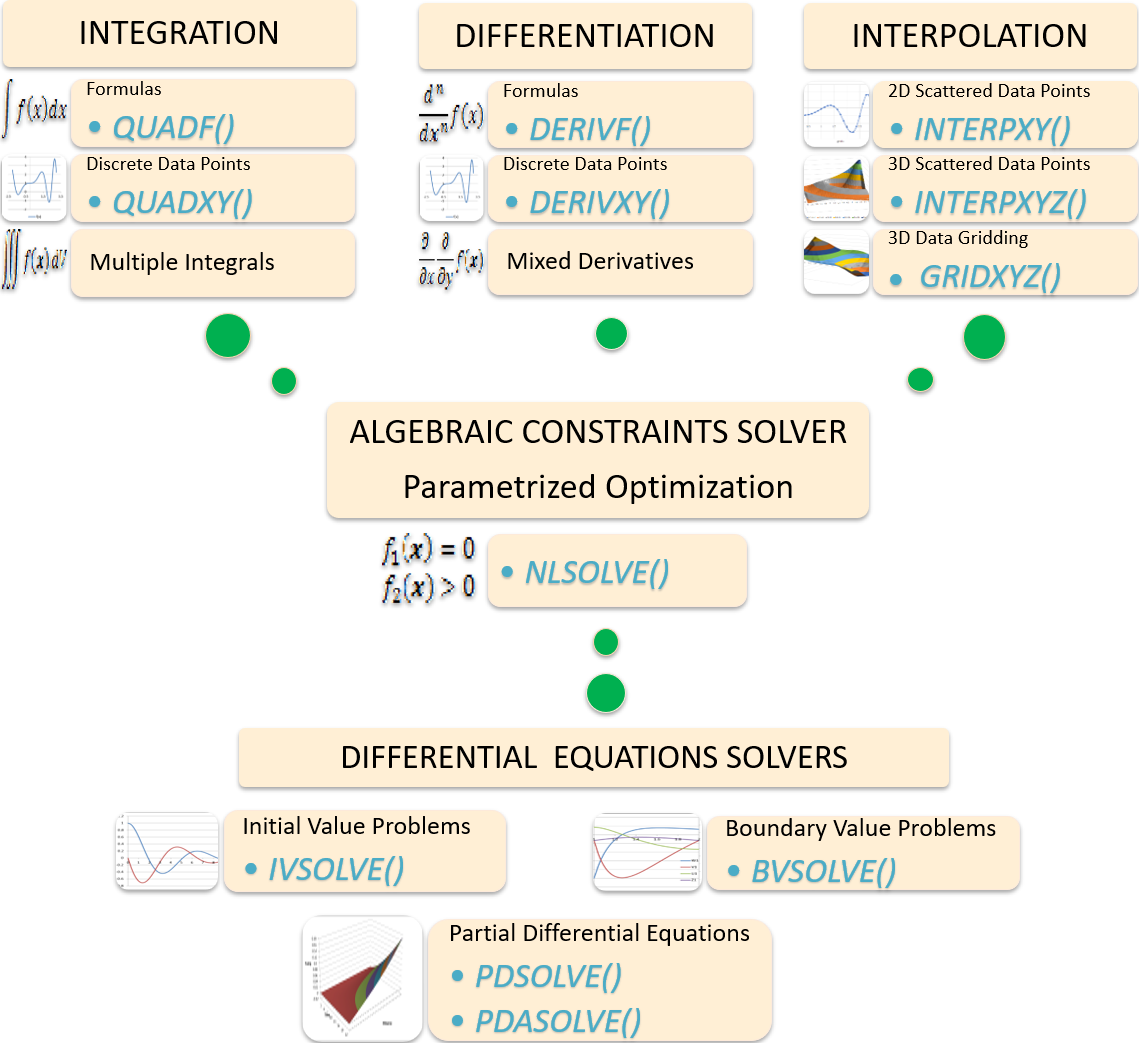
Integration

How to compute numerical integrals with QUADF()

Description

This video demonstrates how to use the integration functions QUADF for computing accurate integrals in both Excel and Google Sheets. Several examples are solved including fixed limits, infinite limits and singular points. The video also demonstrates how to nest QUADF to compute multiple integrals of any order.

How to compute an (x,y) graph integral with QUADXY()

Description

This video demonstrates how to use the function QUADXY to compute accurate integral of a graph generated from discrete (x,y) data set points in both Excel and Google Sheets by the aid of splines.

Differentiation

How to compute accurate numerical derivatives with DERIVF()

Description

This video demonstrates how to use the function DERIVF to compute first and higher order derivatives of any function in both Excel and Google Sheets. The video also demonstrates how to nest DERIVF to compute mixed and partial derivatives of any order

How to differentiate an (x,y) graph with DERIVXY()

Description

This video demonstrates how to use the function DERIVXY to compute first and higher order derivatives of a graph generated from discrete (x,y) data set points in both Excel and Google Sheets.

Interpolation

How to interpolate (x,y) data points with INTERPXY()

Description

This video demonstrates how to use the function INTERPXY to interpolate on a graph generated from discrete (x,y) data set points in both Excel and Google Sheets by the ais of splines.

How to interpolate from a set of (x,y,z) points with INTERPXYZ()

Description

This video demonstrates how to use the function INTERPXYZ to interpolate from a set of discrete (x,y,z) data points in both Excel and Google Sheets. INTERPXYZ is based on natural neighbor algorithm.

How to plot interpolate and plot surface from scattered (x,y,z) data points with GRIDXYZ()

Description

This video demonstrates how to use the function GRIDXYZ to interpolate a set of scattered (x,y,z) data points onto a uniform rectilinear grid in both Excel and Google Sheets. And, how to generate a surface plot in Excel using the interpolated grid data. GRIDXYZ is based on natural neighbor algorithm.

Differential Equations

How to solve an initial-value ode system with IVSOLVE()

Description

This video demonstrates how to use the function IVSOLVE to solve nonlinear initial value ordinary differential equations in both Excel and Google Sheets.

How to solve a boundary-value ode system with BVSOLVE()

Description

This video demonstrates how to use the function BVSOLVE to solve higher-order nonlinear boundary-value ordinary differential equations in both Excel and Google Sheets.

How to solve a PDE system with PDSOLVE()

Description

This video demonstrates how to use the function PDSOLVE to solve nonlinear partial differential equations in both Excel and Google Sheets. PDSOLVE is based on the Method of Lines.

Equation Systems and Curve Fitting

How to solve a system of equations with NLSOLVE()

Description

This video demonstrates how to use the function NLSOLVE to solve nonlinear equation systems in both Excel and Google Sheets. Multiple examples are illustrated including a system with inequality equation and a parameterized integral problem. NLSOLVE is based on Levenberg, Marquardt algorithm.

How to find best fitting curve for (x,y) data points with NLSOLVE()

Description

This video demonstrates how to use the function NLSOLVE to find least-squares best fitting curve for a set of (x,y) data points in both Excel and Google Sheets. NLSOLVE is based on Levenberg, Marquardt algorithm.
Why should you work with us

Our product is engineered with over two-decades experience in computational calculus. ExceLab add-in is based on an innovative patented technology that represents a breakthrough in the utilization of the spreadsheet application with natural extension of native math functions to calculus. ExceLab functions are unique and have no parallels in the history of the spreadsheet application since its inception in the seventies.

ExceLab the simpler alternative to heavy-weight tools

About Us

  • We stand behind our product which stands on its own merits.

  • We help you with fast and effective support from our expert staff.

  • We deliver timely fixes to your issues.

  • We listen to your needs. Get involved in shaping the next release with features that matter to you.

About ExceLab

  • lightweight efficient library with one click installation and you are up and running.

  • State of the art proven algorithms that work. Best default settings yet you have full control with optional arguments.

  • Get rapid solutions to elementary and advanced calculus problems effortlessly with simple formulas in familiar Excel. Leave tedious coding and expensive complex tools behind

  • Flexible licensing plans that suit your needs.

We invite you to explore the solved problems in the manual and evaluate freely to experience the difference for yourself.

Teach your class with ExceLab

  • Excel is virtually on every computer. Very easy to learn the basics and use.

  • Help your students spend their time solving problems, not figuring out how to use complex tools.

  • Intutive yet powerful differential equations solvers and integrated optimization.

  • Simplified effective approach to optimal control problems for Engineering and Social Studies.

Contact us for practical arrangements that suit your requirements.

ExceLab functions at a glance
Start your free ExceLab evaluation
Question or Comment? Email us:
support @ excel-works.com

ExceLab: Transforming Excel into a Calculus Power House

ExceLab functions and methods are protected by USA Patents 10628634, 10114812, 9892108 and 9286286.

Share
© 2015-2024, ExcelWorks LLC
Boston, USA