$$\underset{1}{\overset{2}{\int }}\frac{2x^5-x+3}{x^2}\cdot dx=9-ln2$$

Solution

We define the integrand formula in A1 using X1 as variable. Excel reports the error #DIV/0! for the formula in A1 since X1 is undefined. This error can be ignored since X1 serves only as a dummy variable for the integrand function and its value is irrelevant for the integration computed in A2.

$$\underset{0}{\overset{1}{\int }}\frac{lnx}{\sqrt{x}}\cdot dx=-4$$

Solution

• We define the integrand formula in A3 using X1 as variable. Excel reports the error #NUM! for the formula in A1 since X1 is undefined. This error can be ignored since X1 serves only as a dummy variable for the integrand function and its value is irrelevant for the integration computed in A4.
• We use QUADF optional parameter number 5 to specify the QAGS algorithm for better accuracy given that there is a singularity at 0.

$$\underset{0}{\overset{1}{\int }}{|x-\frac{1}{7}|}^{-\frac{1}{7}}\cdot {|x-\frac{2}{3}|}^{-\frac{11}{20}}\cdot dx$$

Solution

The integrand in this example has two singularities at $\frac{1}{7}$ and $\frac{11}{20}$. We make use of optional argument 6 to pass the singular points which are defined in vector B5:B6. Note that we skip over optional argument 5 since we do not alter any defaults.

We could pass the singular points in argument 6 using constant array syntax {0.1428571, 0.55}, but we would lose some accuracy rounding 1/7.

$$\underset{0}{\overset{\infty }{\int }}\frac{1}{1+x^2}\cdot dx=\frac{\pi }{2}$$

Solution

$$\underset{-\infty }{\overset{\infty }{\int }}{e}^{-x^2}\cdot dx=\sqrt{\pi }$$

Solution

We demonstrate how to integrate a user defined VBA function with QUADF. You can define your own VBA functions in Excel which is quite powerful when your integrand is difficult to define with standard formulas. We will compute the integral

\underset{1}{\overset{2}{\int }}log(x+p)\cdot dx, where p is a constant parameter.

VBA is supported in ExceLab 7.0 only. ExceLab 365 which is based on cross-platform Office JS technology is not compatible with VBA

Solution

1. Open Excel and start VBA Editor by pressing Alt+F11

2. Insert a Module from the Insert Tab, then code the following function:

   

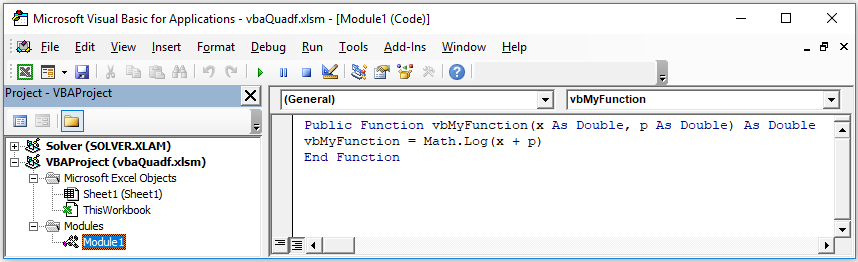
3. Save the workbook with the extension xlsm (macro enabled) and close VBA editor
4. In Sheet1, define your integrand formula as shown in A11.We pass the integration variable and any other parameters the VBA function expects.

Your VBA function name must be prefixed with "vb" to be used with ExceLab solvers.

X1 is just a dummy variable for the integrand function. Its value is ignored.