Quadratic Control Problem with Integral Constraint
The following example was demonstrated by Liu et al. [1] who showed the that the optimal control can be calculated by solving an optimal parameter selection problem together with an unconstrained LQ problem. The optimal control problem is stated as follows:
Find 
which
|
minimize the cost index |
|
|---|---|
|
|
(1) |
|
subject to |
|
|
|
(2) |
|
|
(3) |
|
with initial conditions |
|
|
|
(4) |
|
and integral bounds constraint |
|
|
|
(5) |
,
,
,
,
.Liu et al. [1] calculated, with aid of control software MISER 3.1, an optimal cost index J of 62.66103.
Spreadsheet Model
Referring to Figure 1, we model the problem in Excel working with named variables shown in column A. We parametrize both u1(t)
and u2(t) using 3rd-order polynomials as shown in B10 and B11. We obtain an initial solution to the underlining initial value problem (2)-(4)
by evaluating the array formula =IVSOLVE(B13:B14, B2:B4, {0,1})
in an allocated array E1:G102 shown partially in Figure 2.
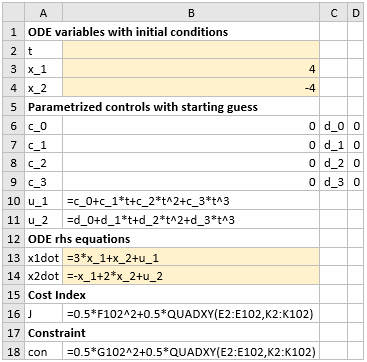
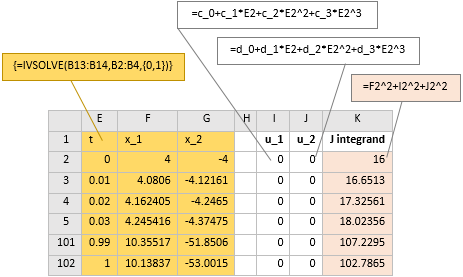
To define the formula for the cost index (1), we generate values for the controls formulas, and the integrand expression for the cost index as shown in columns I, J, and K of Figure 2. Next, we define an analog formula for the cost index (1) using QUADXY to integrate the integrand column K2:K102 with respect to the time column E2:E102 as shown in B16. Similarly, we define an analog formula for the integral constraint (5) as shown in B18. We have completed all the input needed to run Excel Solver.
Results and Analysis
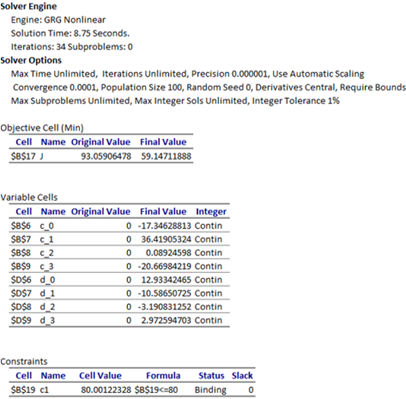
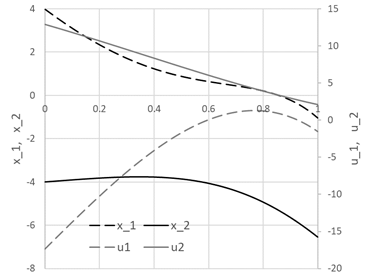
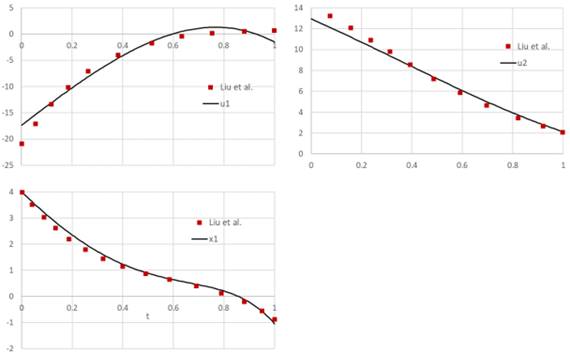
We configure Excel Solver to minimize the cost index B16 by varying the controls coefficients B6:B9 and D6:D9, subject to the integral constraint B18 ≤ 80. Excel Solver converges in approximately 8 seconds to the solution shown in Figure 3 and plotted in Figure 4. The obtained cost index at 59.1471 is lower than reported by Liu et al. [1] at 62.66103. In Figure 5, we provide direct comparisons for x1(t), u1(t) and u2(t) trajectories obtained by the current method and digitized plot values from [1]. The plots show good agreement despite fundamentally different solution strategies.
References
[1] A. E. B. Lim, Y. Q. Liu, K. L. Teo, and Moore J. B. Linear-quadratic optimal control with integral quadratic constraints. Optimal control and applications and methods, 20:79-92, 1999.
[2] Ghaddar, C.K. "Rapid Solution of Optimal Control Problems by a Functional Spreadsheet Paradigm: A Practical Method for the Non-Programmer". Math. Comput. Appl. 2018, 23, 54.
Available at: https://www.mdpi.com/2297-8747/23/4/54
[3] Ghaddar, C. K. "Novel Spreadsheet Direct Method for Optimal Control Problems." Math. Comput. Appl., 23, 6, 2018.
Available at: http://www.mdpi.com/2297-8747/23/1/6
